| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 4 (Before Exercise 12.1) | Exercise 12.1 | Example 5 to 7 (Before Exercise 12.2) |
| Exercise 12.2 | ||
Chapter 12 Surface Areas And Volumes
Welcome to the comprehensive solutions guide for Chapter 12, "Surface Areas And Volumes," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This chapter significantly extends the mensuration concepts learned in Class 9, focusing on more complex scenarios involving combinations of basic three-dimensional solids and the conversion of solids from one shape to another. These advanced applications require a strong grasp of the fundamental formulas for surface area and volume and the ability to visualize and analyze composite structures. Mastering these skills is crucial for tackling practical problems in various scientific and engineering domains. These solutions provide detailed, step-by-step methods and clear explanations to ensure students can confidently navigate these complexities.
A primary focus of this chapter is dealing with solid figures formed by combining two or more basic solids, such as cubes, cuboids, cylinders, cones, spheres, and hemispheres. The solutions demonstrate systematic approaches for calculating the measurements of these composite solids:
- Total Surface Area (TSA) of Combined Solids: This often requires careful visualization. It's emphasized that the TSA of the combined solid is not simply the sum of the individual TSAs of the constituent solids. Instead, one must identify only the exposed surfaces of the final object. For example, when a cone is mounted on a hemisphere, the base of the cone and the circular top of the hemisphere are joined and thus not part of the exposed surface area. The TSA is calculated by summing the areas of only these external surfaces (e.g., CSA of cone + CSA of hemisphere). Solutions meticulously guide students in identifying these relevant surface areas.
- Volume of Combined Solids: Calculating the volume of composite solids is generally more straightforward. The solutions demonstrate that the total volume is typically found by simply adding the volumes of the individual constituent solids (e.g., Volume of capsule = Volume of cylinder + 2 $\times$ Volume of hemisphere).
Another major theme explored is the Conversion of Solids from one shape into another. This concept applies to processes like melting a metallic object and recasting it into a different shape (e.g., melting a sphere to form a wire/cylinder, or melting a large cone to form smaller cones). The fundamental principle applied in these problems, and clearly illustrated in the solutions, is the conservation of volume. It is assumed that the volume of the material remains constant during the transformation. Therefore, the solutions demonstrate setting up an equation where the volume of the original solid is equated to the volume of the new solid (or the sum of volumes if multiple objects are formed: $V_{\text{original}} = V_{\text{new}}$ or $V_{\text{original}} = n \times V_{\text{new object}}$). This equation is then solved to find unknown dimensions (like radius, height, or the number of smaller objects formed). Careful application of the correct volume formulas is essential.
Throughout the solutions, consistent emphasis is placed on the accurate application of formulas, meticulous handling of dimensions (radius $r$, height $h$, slant height $l = \sqrt{r^2+h^2}$ for cones), and maintaining unit consistency, including necessary conversions (e.g., between cm, m, or relating volume to capacity in liters, possibly involving costs in $\textsf{₹}$). Practical word problems often require careful reading to determine whether surface area or volume is required and to extract all necessary dimensional information.
Regarding the rationalized syllabus for 2024-25, Chapter 12, "Surface Areas And Volumes" (formerly Chapter 13), has undergone a significant change. The entire section dealing with the Frustum of a Cone (including its surface area and volume formulas and all related exercises) has been completely removed from the Class 10 curriculum. The chapter now focuses exclusively on problems involving the surface area and volume of combinations of the basic solids (cube, cuboid, cylinder, cone, sphere, hemisphere) and the conversion of solids based on volume conservation. By diligently working through these focused solutions, students can master the techniques for calculating measures of combined solids, understand and apply the principle of volume conservation, and confidently solve complex, real-world mensuration problems involving these fundamental shapes.
Example 1 to 4 (Before Exercise 12.1)
Example 1. Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (see Fig 12.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = $\frac{22}{7}$ )
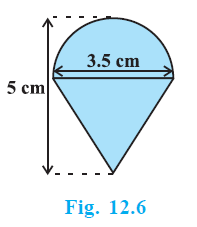
Answer:
Given:
Total height of the top = $5 \text{ cm}$
Diameter of the top = $3.5 \text{ cm}$
Value of $\pi = \frac{22}{7}$
To Find:
The area Rasheed has to colour (Total surface area of the top).
Solution:
The top is in the shape of a cone surmounted by a hemisphere. The area to be coloured is the sum of the curved surface area (CSA) of the hemisphere and the curved surface area (CSA) of the cone.
The diameter of the top is $3.5 \text{ cm}$, so the radius is half of the diameter.
Radius, $r = \frac{3.5}{2} \text{ cm} = 1.75 \text{ cm}$
The height of the hemisphere is equal to its radius, which is $1.75 \text{ cm}$.
The total height of the top is $5 \text{ cm}$.
The height of the cone, $h = \text{Total height} - \text{Height of hemisphere}$
$h = 5 \text{ cm} - 1.75 \text{ cm} = 3.25 \text{ cm}$
Curved Surface Area (CSA) of the Hemisphere:
The formula for the CSA of a hemisphere is $2\pi r^2$.
CSA of hemisphere $= 2 \times \frac{22}{7} \times (1.75 \text{ cm})^2$
$= 2 \times \frac{22}{7} \times (1.75) \times (1.75) \text{ cm}^2$
We can write $1.75 = \frac{175}{100} = \frac{7}{4}$.
CSA of hemisphere $= 2 \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \text{ cm}^2$
$= \cancel{2}^{1} \times \frac{22}{\cancel{7}^{1}} \times \frac{\cancel{7}^{1}}{\cancel{4}^{2}} \times \frac{7}{4} \text{ cm}^2$
$= \frac{22 \times 7}{2 \times 4} \text{ cm}^2$
$= \frac{\cancel{154}^{77}}{\cancel{8}^{4}} \text{ cm}^2$
$= \frac{77}{4} \text{ cm}^2 = 19.25 \text{ cm}^2$
Curved Surface Area (CSA) of the Cone:
The formula for the CSA of a cone is $\pi r l$, where $l$ is the slant height.
The slant height $l$ is given by the formula $l = \sqrt{r^2 + h^2}$.
$r = 1.75 \text{ cm}$ and $h = 3.25 \text{ cm}$.
$r^2 = (1.75)^2 = 3.0625$
$h^2 = (3.25)^2 = 10.5625$
$l = \sqrt{3.0625 + 10.5625} = \sqrt{13.625}$
For calculation purposes, we use the approximate value of $l \approx 3.7 \text{ cm}$ (as is standard for this problem). Note that $3.7^2 = 13.69$, which is close to $13.625$.
CSA of cone $= \pi r l = \frac{22}{7} \times 1.75 \text{ cm} \times 3.7 \text{ cm}$
Using $1.75 = \frac{7}{4}$:
CSA of cone $= \frac{22}{7} \times \frac{7}{4} \times 3.7 \text{ cm}^2$
$= \frac{\cancel{22}^{11}}{\cancel{7}^{1}} \times \frac{\cancel{7}^{1}}{\cancel{4}^{2}} \times 3.7 \text{ cm}^2$
$= \frac{11}{2} \times 3.7 \text{ cm}^2$
$= 5.5 \times 3.7 \text{ cm}^2$
$= 20.35 \text{ cm}^2$
Total Area to be Coloured:
Total Area = CSA of hemisphere + CSA of cone
$= 19.25 \text{ cm}^2 + 20.35 \text{ cm}^2$
$= 39.60 \text{ cm}^2$
Answer:
The area Rasheed has to colour is $39.60 \text{ cm}^2$.
Example 2. The decorative block shown in Fig. 12.7 is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take π = $\frac{22}{7}$ )
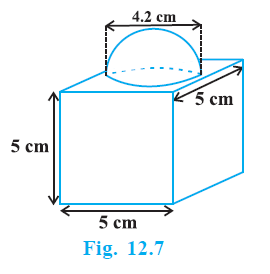
Answer:
Given:
Edge of the cube, $a = 5 \text{ cm}$
Diameter of the hemisphere, $d = 4.2 \text{ cm}$
Value of $\pi = \frac{22}{7}$
To Find:
The total surface area of the block.
Solution:
The decorative block consists of a cube and a hemisphere fixed on top of it. The total surface area of the block is the sum of the surface area of the cube and the surface area of the hemisphere. However, since the base of the hemisphere is fixed on the top face of the cube, the area of the base of the hemisphere is not exposed and the area of the top face of the cube covered by the hemisphere is also not exposed.
Total Surface Area of the block = Surface Area of Cube - Area of the base of the hemisphere + Curved Surface Area of the hemisphere.
Surface Area of the Cube:
The formula for the surface area of a cube with edge $a$ is $6a^2$.
Surface Area of Cube $= 6 \times (5 \text{ cm})^2$
$= 6 \times 25 \text{ cm}^2$
$= 150 \text{ cm}^2$
Radius of the Hemisphere:
The diameter of the hemisphere is $d = 4.2 \text{ cm}$.
Radius of hemisphere, $r = \frac{d}{2} = \frac{4.2}{2} \text{ cm} = 2.1 \text{ cm}$
Area of the base of the hemisphere:
The base of the hemisphere is a circle with radius $r = 2.1 \text{ cm}$.
Area of base of hemisphere $= \pi r^2 = \frac{22}{7} \times (2.1 \text{ cm})^2$
$= \frac{22}{7} \times 2.1 \times 2.1 \text{ cm}^2$
$= 22 \times \frac{\cancel{2.1}^{0.3}}{\cancel{7}^{1}} \times 2.1 \text{ cm}^2$
$= 22 \times 0.3 \times 2.1 \text{ cm}^2$
$= 6.6 \times 2.1 \text{ cm}^2$
$= 13.86 \text{ cm}^2$
Curved Surface Area (CSA) of the Hemisphere:
The formula for the CSA of a hemisphere is $2\pi r^2$.
CSA of hemisphere $= 2 \times \frac{22}{7} \times (2.1 \text{ cm})^2$
$= 2 \times \frac{22}{7} \times 2.1 \times 2.1 \text{ cm}^2$
$= 2 \times 13.86 \text{ cm}^2$ (Since $\pi r^2 = 13.86$)
$= 27.72 \text{ cm}^2$
Total Surface Area of the block:
Total SA $= \text{Area of 5 faces of cube} + \text{Area of top face of cube (excluding hemisphere base)} + \text{CSA of hemisphere}$
This can be calculated as:
Total SA $= \text{Surface Area of Cube} - \text{Area of base of hemisphere} + \text{CSA of hemisphere}$
$= 150 \text{ cm}^2 - 13.86 \text{ cm}^2 + 27.72 \text{ cm}^2$
$= 150 \text{ cm}^2 + (27.72 - 13.86) \text{ cm}^2$
$= 150 \text{ cm}^2 + 13.86 \text{ cm}^2$
$= 163.86 \text{ cm}^2$
Answer:
The total surface area of the block is $163.86 \text{ cm}^2$.
Example 3. A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in Fig. 12.8. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)
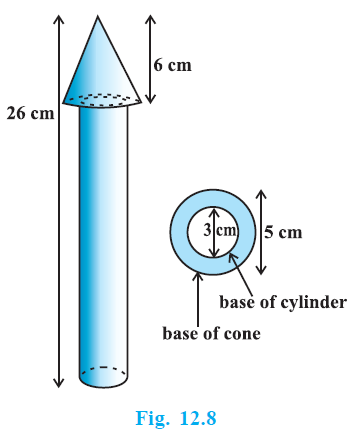
Answer:
Given:
Total height of the rocket = $26 \text{ cm}$
Height of the conical part, $h_c = 6 \text{ cm}$
Diameter of the base of the conical part = $5 \text{ cm}$
Diameter of the base of the cylindrical part = $3 \text{ cm}$
Value of $\pi = 3.14$
To Find:
Area painted orange (conical part) and area painted yellow (cylindrical part).
Solution:
The rocket consists of a cone mounted on a cylinder.
Conical Part (Painted Orange):
Diameter of cone base = $5 \text{ cm}$. Radius of cone base, $r_c = \frac{5}{2} \text{ cm} = 2.5 \text{ cm}$.
Height of conical part, $h_c = 6 \text{ cm}$.
The area to be painted orange is the curved surface area (CSA) of the cone plus the area of the base of the cone that is exposed (which is an annulus, as the cylindrical part is below it). However, the problem states "conical portion is to be painted orange", implying the visible surface area of the conical part when it's on top of the cylinder. This would be the CSA of the cone plus the area of the conical base minus the area of the cylindrical top that is covered by the conical base. A simpler interpretation is the CSA of the cone plus the area of the base of the cone (which is not covered by anything above or below).
Let's assume the conical portion means the entire conical shape, and it is attached to the cylinder such that the cylinder's top surface is below the cone's base. The exposed orange area is the CSA of the cone + (Area of base of cone - Area of top of cylinder).
Slant height of cone, $l = \sqrt{r_c^2 + h_c^2}$
$l = \sqrt{(2.5)^2 + (6)^2} = \sqrt{6.25 + 36} = \sqrt{42.25} \text{ cm}$
$l = 6.5 \text{ cm}$
CSA of cone $= \pi r_c l = 3.14 \times 2.5 \text{ cm} \times 6.5 \text{ cm}$
$= 3.14 \times 16.25 \text{ cm}^2$
$= 50.875 \text{ cm}^2$
Area of cone base $= \pi r_c^2 = 3.14 \times (2.5 \text{ cm})^2 = 3.14 \times 6.25 \text{ cm}^2$
$= 19.625 \text{ cm}^2$
Diameter of cylinder base = $3 \text{ cm}$. Radius of cylinder base, $r_y = \frac{3}{2} \text{ cm} = 1.5 \text{ cm}$.
Area of cylinder top $= \pi r_y^2 = 3.14 \times (1.5 \text{ cm})^2 = 3.14 \times 2.25 \text{ cm}^2$
$= 7.065 \text{ cm}^2$
Area painted orange = CSA of cone + (Area of cone base - Area of cylinder top)
$= 50.875 \text{ cm}^2 + (19.625 \text{ cm}^2 - 7.065 \text{ cm}^2)$
$= 50.875 \text{ cm}^2 + 12.56 \text{ cm}^2$
$= 63.435 \text{ cm}^2$
Cylindrical Part (Painted Yellow):
Radius of cylinder, $r_y = 1.5 \text{ cm}$.
Total height of rocket = $26 \text{ cm}$. Height of conical part = $6 \text{ cm}$.
Height of cylindrical part, $h_y = \text{Total height} - \text{Height of conical part}$
$h_y = 26 \text{ cm} - 6 \text{ cm} = 20 \text{ cm}$.
The area to be painted yellow is the curved surface area (CSA) of the cylinder plus the area of the base of the cylinder (which rests on the ground).
CSA of cylinder $= 2\pi r_y h_y = 2 \times 3.14 \times 1.5 \text{ cm} \times 20 \text{ cm}$
$= 2 \times 3.14 \times 30 \text{ cm}^2$
$= 6.28 \times 30 \text{ cm}^2$
$= 188.4 \text{ cm}^2$
Area of cylinder base $= \pi r_y^2 = 3.14 \times (1.5 \text{ cm})^2 = 3.14 \times 2.25 \text{ cm}^2$
$= 7.065 \text{ cm}^2$
Area painted yellow = CSA of cylinder + Area of cylinder base
$= 188.4 \text{ cm}^2 + 7.065 \text{ cm}^2$
$= 195.465 \text{ cm}^2$
Answer:
Area painted orange $= 63.435 \text{ cm}^2$.
Area painted yellow $= 195.465 \text{ cm}^2$.
Example 4. Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (see Fig. 12.9). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath. (Take π = $\frac{22}{7}$ )
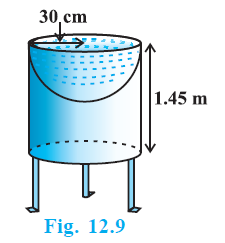
Answer:
This problem involves finding the total surface area of a composite solid shape, which is a cylinder with a hemispherical depression at the top. We need to combine the surface areas of the cylindrical and hemispherical parts.
Given:
Height of the cylinder, $h = 1.45 \text{ m}$
Radius of the cylinder, $r = 30 \text{ cm}$
Hemispherical depression at one end.
Value of $\pi = \frac{22}{7}$
To Find:
The total surface area of the bird-bath.
Solution:
The bird-bath consists of a cylindrical part and a hemispherical depression. The radius of the hemispherical depression is the same as the radius of the cylinder, $r = 30 \text{ cm}$.
First, ensure all units are consistent. Convert the height of the cylinder from meters to centimeters: $h = 1.45 \text{ m} = 1.45 \times 100 \text{ cm} = 145 \text{ cm}$.
The total surface area of the bird-bath consists of the curved surface area of the cylindrical part and the curved surface area of the hemispherical depression. The base of the cylinder is assumed to be resting on the ground, so its area is typically not included in the 'total surface area' in this context.
Total Surface Area = Curved Surface Area (CSA) of cylinder + Curved Surface Area (CSA) of hemisphere
The formula for the CSA of a cylinder is $2\pi r h$.
The formula for the CSA of a hemisphere is $2\pi r^2$.
Total Surface Area $= 2\pi r h + 2\pi r^2$
We can take $2\pi r$ common from both terms:
Total Surface Area $= 2\pi r (h + r)$
Now, substitute the given values: $r = 30 \text{ cm}$, $h = 145 \text{ cm}$, and $\pi = \frac{22}{7}$.
Total Surface Area $= 2 \times \frac{22}{7} \times 30 \text{ cm} \times (145 \text{ cm} + 30 \text{ cm})$
$= \frac{44}{7} \times 30 \text{ cm} \times (175 \text{ cm})$
$= \frac{1320}{7} \times 175 \text{ cm}^2$
We can cancel out the common factor of 7 from the denominator and 175 in the numerator:
$175 \div 7 = 25$.
Total Surface Area $= 1320 \times 25 \text{ cm}^2$
Multiply $1320$ by $25$:
$1320 \times 25 = 33000$
Total Surface Area $= 33000 \text{ cm}^2$
The question asks for the area in terms of the given units (m for height, cm for radius). It's useful to provide the answer in both cm$^2$ and m$^2$.
To convert from cm$^2$ to m$^2$, we divide by $100^2 = 10000$, because $1 \text{ m} = 100 \text{ cm}$, so $1 \text{ m}^2 = 100 \text{ cm} \times 100 \text{ cm} = 10000 \text{ cm}^2$.
Total Surface Area in m$^2 = \frac{33000}{10000} \text{ m}^2$
$= 3.3 \text{ m}^2$
Answer:
The total surface area of the bird-bath is $33000 \text{ cm}^2$ or $3.3 \text{ m}^2$.
Exercise 12.1
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Answer:
This problem involves joining two cubes to form a cuboid and calculating the surface area of the resulting shape.
Given:
Volume of each of the two cubes = $64 \text{ cm}^3$.
The two cubes are joined end to end.
To Find:
The surface area of the resulting cuboid.
Solution:
Let the side length of each cube be $a$.
The volume of a cube is given by the formula $V = a^3$.
We are given that the volume of each cube is $64 \text{ cm}^3$.
$a^3 = 64 \text{ cm}^3$
... (i)
To find the side length $a$, we take the cube root of the volume:
$a = \sqrt[3]{64} \text{ cm}$
$a = 4 \text{ cm}$
When two such cubes are joined end to end, they form a cuboid. The dimensions of this cuboid will change in one direction (the direction they are joined). The length becomes the sum of the side lengths of the two cubes, while the breadth and height remain the same as the side length of a single cube.
Length of the resulting cuboid, $L = a + a = 2a$
Breadth of the resulting cuboid, $B = a$
Height of the resulting cuboid, $H = a$
Substituting the value $a = 4 \text{ cm}$:
$L = 2 \times 4 \text{ cm} = 8 \text{ cm}$
$B = 4 \text{ cm}$
$H = 4 \text{ cm}$
The dimensions of the resulting cuboid are $8 \text{ cm} \times 4 \text{ cm} \times 4 \text{ cm}$.
The formula for the surface area of a cuboid with length $L$, breadth $B$, and height $H$ is:
Surface Area $= 2(LB + BH + HL)$
Substitute the dimensions of the resulting cuboid into the formula:
Surface Area $= 2((8 \text{ cm})(4 \text{ cm}) + (4 \text{ cm})(4 \text{ cm}) + (4 \text{ cm})(8 \text{ cm}))$
Surface Area $= 2(32 \text{ cm}^2 + 16 \text{ cm}^2 + 32 \text{ cm}^2)$
First, sum the areas inside the bracket:
$32 + 16 + 32 = 80 \text{ cm}^2$
Now, multiply by 2:
Surface Area $= 2(80 \text{ cm}^2) = 160 \text{ cm}^2$
Answer:
The surface area of the resulting cuboid is $160 \text{ cm}^2$.
Question 2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Answer:
This problem asks for the inner surface area of a vessel shaped like a hollow hemisphere topped by a hollow cylinder. The inner surface area includes the curved surfaces exposed to the inside.
Given:
The vessel is in the form of a hollow hemisphere mounted by a hollow cylinder.
Diameter of the hemisphere = $14 \text{ cm}$
Total height of the vessel = $13 \text{ cm}$
Value of $\pi = \frac{22}{7}$
To Find:
The inner surface area of the vessel.
Solution:
The inner surface area of the vessel is the sum of the inner curved surface area (CSA) of the hemisphere and the inner curved surface area (CSA) of the cylinder. The base of the hemisphere is closed, and the top of the cylinder is open (as it's a vessel). The area where the hemisphere and cylinder join is not part of the inner surface area.
Diameter of the hemisphere = $14 \text{ cm}$.
Radius of the hemisphere, $r = \frac{\text{Diameter}}{2} = \frac{14}{2} \text{ cm} = 7 \text{ cm}$.
Since the cylinder is mounted on the hemisphere and is hollow, the base of the cylinder aligns with the top of the hemisphere and has the same radius.
Radius of the cylinder, $r = 7 \text{ cm}$.
The total height of the vessel is $13 \text{ cm}$. The height of the hemispherical part is equal to its radius, which is $7 \text{ cm}$.
Height of the cylindrical part, $h = \text{Total height of vessel} - \text{Height of hemisphere}$
$h = 13 \text{ cm} - 7 \text{ cm} = 6 \text{ cm}$.
Inner CSA of the Hemisphere:
The formula for the inner CSA of a hollow hemisphere is $2\pi r^2$.
Inner CSA of hemisphere $= 2 \times \frac{22}{7} \times (7 \text{ cm})^2$
$= 2 \times \frac{22}{7} \times 49 \text{ cm}^2$
$= 2 \times 22 \times \frac{\cancel{49}^{7}}{\cancel{7}^{1}} \text{ cm}^2$
$= 44 \times 7 \text{ cm}^2 = 308 \text{ cm}^2$
Inner CSA of the Cylinder:
The formula for the inner CSA of a hollow cylinder is $2\pi r h$.
Inner CSA of cylinder $= 2 \times \frac{22}{7} \times 7 \text{ cm} \times 6 \text{ cm}$
$= 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{7}^{1} \times 6 \text{ cm}^2$
$= 2 \times 22 \times 6 \text{ cm}^2 = 44 \times 6 \text{ cm}^2 = 264 \text{ cm}^2$
Total Inner Surface Area of the Vessel:
Total Inner SA = Inner CSA of hemisphere + Inner CSA of cylinder
$= 308 \text{ cm}^2 + 264 \text{ cm}^2 = 572 \text{ cm}^2$
Answer:
The inner surface area of the vessel is $572 \text{ cm}^2$.
Question 3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer:
This problem asks for the total surface area of a toy shaped like a cone placed on top of a hemisphere. The surface area includes the exposed curved surfaces of both parts.
Given:
The toy is in the form of a cone mounted on a hemisphere.
Radius of the cone = Radius of the hemisphere, $r = 3.5 \text{ cm}$.
Total height of the toy = $15.5 \text{ cm}$.
Value of $\pi = \frac{22}{7}$
To Find:
The total surface area of the toy.
Solution:
The total surface area of the toy is the sum of the curved surface area (CSA) of the cone and the curved surface area (CSA) of the hemisphere. The base of the cone is joined to the hemisphere and is not part of the exposed surface area.
Radius of hemisphere, $r = 3.5 \text{ cm}$.
Radius of cone, $r = 3.5 \text{ cm}$.
The height of the hemispherical part is equal to its radius, which is $3.5 \text{ cm}$.
The total height of the toy is $15.5 \text{ cm}$.
Height of the conical part, $h = \text{Total height of toy} - \text{Height of hemisphere}$
$h = 15.5 \text{ cm} - 3.5 \text{ cm} = 12 \text{ cm}$.
Curved Surface Area (CSA) of the Hemisphere:
The formula for the CSA of a hemisphere is $2\pi r^2$.
CSA of hemisphere $= 2 \times \frac{22}{7} \times (3.5 \text{ cm})^2$
$= 2 \times \frac{22}{7} \times (3.5) \times (3.5) \text{ cm}^2$
$= 44 \times \frac{\cancel{3.5}^{0.5}}{\cancel{7}^{1}} \times 3.5 \text{ cm}^2$
$= 44 \times 0.5 \times 3.5 \text{ cm}^2$
$= 22 \times 3.5 \text{ cm}^2 = 77 \text{ cm}^2$
Curved Surface Area (CSA) of the Cone:
The formula for the CSA of a cone is $\pi r l$, where $l$ is the slant height. We need to calculate the slant height first.
The slant height $l$ is given by the formula $l = \sqrt{r^2 + h^2}$.
Using $r = 3.5 \text{ cm}$ and $h = 12 \text{ cm}$:
$l = \sqrt{(3.5)^2 + (12)^2} = \sqrt{12.25 + 144} = \sqrt{156.25} \text{ cm}$
The square root of $156.25$ is $12.5$.
$l = 12.5 \text{ cm}$
Now, calculate the CSA of the cone:
CSA of cone $= \pi r l = \frac{22}{7} \times 3.5 \text{ cm} \times 12.5 \text{ cm}$
$= \frac{22}{\cancel{7}^{1}} \times \cancel{3.5}^{0.5} \times 12.5 \text{ cm}^2$
$= 22 \times 0.5 \times 12.5 \text{ cm}^2$
$= 11 \times 12.5 \text{ cm}^2 = 137.5 \text{ cm}^2$
Total Surface Area of the toy:
Total SA = CSA of hemisphere + CSA of cone
$= 77 \text{ cm}^2 + 137.5 \text{ cm}^2 = 214.5 \text{ cm}^2$
Answer:
The total surface area of the toy is $214.5 \text{ cm}^2$.
Question 4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Answer:
This problem asks about placing the largest possible hemisphere on top of a cube and finding the total surface area of the combined solid.
Given:
A cubical block of side $7 \text{ cm}$.
It is surmounted by a hemisphere.
Value of $\pi = \frac{22}{7}$
To Find:
1. The greatest diameter the hemisphere can have.
2. The surface area of the solid.
Solution:
1. Greatest diameter of the hemisphere:
For the hemisphere to be the largest possible and sit entirely on the top face of the cube, its base must be a circle that fits exactly within the square top face. The largest circle that can be inscribed in a square has a diameter equal to the side length of the square.
Side of the cube = $7 \text{ cm}$.
Greatest diameter of the hemisphere = Side of the square face of the cube
Greatest diameter $= 7 \text{ cm}$.
The radius of this hemisphere is half of the diameter: $r = \frac{7}{2} \text{ cm} = 3.5 \text{ cm}$.
2. Surface area of the solid:
The surface area of the solid consists of the area of the faces of the cube that are not covered by the hemisphere's base, plus the area of the part of the top face that is not covered, plus the curved surface area of the hemisphere.
Alternatively, we can consider the total surface area of the cube, subtract the area of the base of the hemisphere (which is on the top face of the cube), and then add the curved surface area of the hemisphere.
Surface Area of solid = Surface Area of cube + (Area of top face - Area of base of hemisphere) + Curved Surface Area of hemisphere
This simplifies to: Surface Area of solid = (Total Area of cube) - (Area of base of hemisphere) + (Curved Surface Area of hemisphere)
Surface Area of cube $= 6 \times (\text{side})^2 = 6 \times (7 \text{ cm})^2 = 6 \times 49 \text{ cm}^2 = 294 \text{ cm}^2$.
The base of the hemisphere is a circle with radius $r = 3.5 \text{ cm}$.
Area of base of hemisphere $= \pi r^2 = \frac{22}{7} \times (3.5 \text{ cm})^2 = \frac{22}{7} \times 3.5 \times 3.5 \text{ cm}^2$
$= 22 \times \frac{\cancel{3.5}^{0.5}}{\cancel{7}^{1}} \times 3.5 \text{ cm}^2 = 22 \times 0.5 \times 3.5 \text{ cm}^2 = 11 \times 3.5 \text{ cm}^2 = 38.5 \text{ cm}^2$.
Curved Surface Area (CSA) of hemisphere $= 2\pi r^2 = 2 \times (\text{Area of base of hemisphere})$
$= 2 \times 38.5 \text{ cm}^2 = 77 \text{ cm}^2$.
Now, calculate the total surface area of the solid:
Surface Area of solid $= 294 \text{ cm}^2 - 38.5 \text{ cm}^2 + 77 \text{ cm}^2$
Combine the last two terms first: $77 - 38.5 = 38.5$.
Surface Area of solid $= 294 \text{ cm}^2 + 38.5 \text{ cm}^2 = 332.5 \text{ cm}^2$
Answer:
1. The greatest diameter the hemisphere can have is $7 \text{ cm}$.
2. The surface area of the solid is $332.5 \text{ cm}^2$.
Question 5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer:
This problem involves removing a hemispherical part from a cube and finding the surface area of the remaining solid. The removed part creates a new surface area inside the block.
Given:
A cubical wooden block.
A hemispherical depression is cut out from one face.
The diameter ($l$) of the hemisphere is equal to the edge of the cube.
Value of $\pi$ (use $\frac{22}{7}$ or keep as $\pi$ if the answer is an expression) - The problem does not specify a value, and the result is typically left in terms of $\pi$ when asked to "Determine the surface area" using a variable length like $l$. We will provide the expression in terms of $\pi$ and $l$.
To Find:
The surface area of the remaining solid.
Solution:
Let the edge of the cube be $a$. According to the problem, the diameter of the hemispherical depression is equal to the edge of the cube.
Diameter of hemisphere, $d = l = a$.
Radius of hemisphere, $r = \frac{d}{2} = \frac{l}{2} = \frac{a}{2}$.
The surface area of the remaining solid consists of:
1. The area of the faces of the cube that are untouched (5 faces).
2. The area of the part of the face from which the depression was cut, that remains (Area of the square face - Area of the circular base of the hemisphere).
3. The curved surface area of the hemispherical depression.
Surface Area of remaining solid = (Area of 5 faces of cube) + (Area of 1 face - Area of circular base of hemisphere) + (Curved Surface Area of hemisphere)
This can be simplified as:
Surface Area of remaining solid = Total Surface Area of cube - Area of circular base of hemisphere + Curved Surface Area of hemisphere
Total Surface Area of cube $= 6a^2$. Since $a = l$, this is $6l^2$.
The base of the hemispherical depression is a circle with radius $r = l/2$.
Area of circular base of hemisphere $= \pi r^2 = \pi (\frac{l}{2})^2 = \pi \frac{l^2}{4}$.
Curved Surface Area (CSA) of hemispherical depression $= 2\pi r^2 = 2\pi (\frac{l}{2})^2 = 2\pi \frac{l^2}{4} = \frac{\pi l^2}{2}$.
Substitute these areas into the formula for the surface area of the remaining solid:
Surface Area of remaining solid $= 6l^2 - \frac{\pi l^2}{4} + \frac{\pi l^2}{2}$
Combine the terms with $\pi l^2$:
$\frac{\pi l^2}{2} - \frac{\pi l^2}{4} = \frac{2\pi l^2 - \pi l^2}{4} = \frac{\pi l^2}{4}$
So, Surface Area of remaining solid $= 6l^2 + \frac{\pi l^2}{4}$
We can factor out $l^2$ from the expression:
Surface Area of remaining solid $= l^2 (6 + \frac{\pi}{4})$
Answer:
The surface area of the remaining solid is $6l^2 + \frac{\pi l^2}{4}$ or $l^2 (6 + \frac{\pi}{4})$.
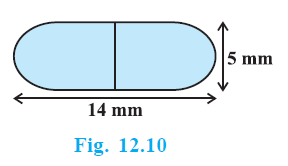
Question 6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 12.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
Answer:
This problem involves calculating the surface area of a medicine capsule, which is a combination of a cylinder and two hemispheres attached to its ends.
Given:
The capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends.
Length of the entire capsule = $14 \text{ mm}$
Diameter of the capsule = $5 \text{ mm}$
Value of $\pi = \frac{22}{7}$
To Find:
The surface area of the capsule.
Solution:
The total surface area of the capsule is the sum of the curved surface area (CSA) of the cylindrical part and the curved surface areas (CSA) of the two hemispherical ends. The flat circular bases of the cylinder and hemispheres are joined internally and are not part of the exposed surface area.
Diameter of the capsule = $5 \text{ mm}$.
Radius of the capsule (which is the radius of the hemisphere and the base of the cylinder), $r = \frac{\text{Diameter}}{2} = \frac{5}{2} \text{ mm} = 2.5 \text{ mm}$.
The height (or length) of each hemispherical part is equal to its radius, which is $2.5 \text{ mm}$.
The total length of the capsule is $14 \text{ mm}$. This includes the length of the cylinder and the heights of the two hemispheres at the ends.
Height (length) of the cylindrical part, $h = \text{Total length of capsule} - (\text{Radius of hemisphere at one end} + \text{Radius of hemisphere at other end})$
$h = 14 \text{ mm} - (2.5 \text{ mm} + 2.5 \text{ mm})$
$h = 14 \text{ mm} - 5 \text{ mm} = 9 \text{ mm}$.
Curved Surface Area (CSA) of the two Hemispheres:
The formula for the CSA of one hemisphere is $2\pi r^2$. Since there are two hemispheres, their combined CSA is $2 \times 2\pi r^2 = 4\pi r^2$.
Combined CSA of two hemispheres $= 4 \times \frac{22}{7} \times (2.5 \text{ mm})^2$
$= \frac{88}{7} \times 6.25 \text{ mm}^2$
$= \frac{88 \times 6.25}{7} \text{ mm}^2 = \frac{550}{7} \text{ mm}^2$
Curved Surface Area (CSA) of the Cylinder:
The formula for the CSA of a cylinder is $2\pi r h$.
Using $r = 2.5 \text{ mm}$ and $h = 9 \text{ mm}$:
CSA of cylinder $= 2 \times \frac{22}{7} \times 2.5 \text{ mm} \times 9 \text{ mm}$
$= \frac{44}{7} \times 2.5 \times 9 \text{ mm}^2$
$= \frac{44 \times 22.5}{7} \text{ mm}^2 = \frac{990}{7} \text{ mm}^2$
Total Surface Area of the capsule:
Total SA = Combined CSA of two hemispheres + CSA of cylinder
$= \frac{550}{7} \text{ mm}^2 + \frac{990}{7} \text{ mm}^2$
Since the denominators are the same, we can add the numerators:
$= \frac{550 + 990}{7} \text{ mm}^2 = \frac{1540}{7} \text{ mm}^2$
Now, perform the division:
$\frac{1540}{7} = 220$
Total SA $= 220 \text{ mm}^2$
Answer:
The surface area of the capsule is $220 \text{ mm}^2$.
Question 7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m2 . (Note that the base of the tent will not be covered with canvas.)
Answer:
This problem involves calculating the surface area of a tent made of canvas, which is a combination of a cylinder and a cone. We then need to find the cost of the canvas.
Given:
The tent is in the shape of a cylinder surmounted by a conical top.
Height of cylindrical part, $h_c = 2.1 \text{ m}$
Diameter of cylindrical part = $4 \text{ m}$
Radius of cylindrical part, $r = \frac{\text{Diameter}}{2} = \frac{4}{2} \text{ m} = 2 \text{ m}$
Slant height of conical top, $l = 2.8 \text{ m}$
Rate of canvas = $\textsf{₹} 500 \text{ per m}^2$
Base of the tent will not be covered with canvas.
Value of $\pi = \frac{22}{7}$
To Find:
1. The area of the canvas used for making the tent.
2. The cost of the canvas.
Solution:
The area of the canvas used for the tent is the sum of the curved surface area (CSA) of the cylindrical part and the curved surface area (CSA) of the conical top. The base of the cylindrical part is on the ground and is not covered by canvas. The top of the cylindrical part is covered by the base of the cone, so that area is not included in the canvas area.
The radius of the base of the conical part is the same as the radius of the cylindrical part.
Radius of cone base, $r = 2 \text{ m}$.
Slant height of cone, $l = 2.8 \text{ m}$.
Area of the canvas:
Area of canvas = CSA of Cylinder + CSA of Cone
Formula for CSA of Cylinder $= 2\pi r h_c$.
CSA of Cylinder $= 2 \times \frac{22}{7} \times 2 \text{ m} \times 2.1 \text{ m}$
$= \frac{44}{7} \times 2 \times 2.1 \text{ m}^2 = \frac{88}{7} \times 2.1 \text{ m}^2$
$= 88 \times \frac{\cancel{2.1}^{0.3}}{\cancel{7}^{1}} \text{ m}^2 = 88 \times 0.3 \text{ m}^2 = 26.4 \text{ m}^2$
Formula for CSA of Cone $= \pi r l$.
CSA of Cone $= \frac{22}{7} \times 2 \text{ m} \times 2.8 \text{ m}$
$= \frac{44}{7} \times 2.8 \text{ m}^2 = 44 \times \frac{\cancel{2.8}^{0.4}}{\cancel{7}^{1}} \text{ m}^2 = 44 \times 0.4 \text{ m}^2 = 17.6 \text{ m}^2$
Total Area of canvas = CSA of Cylinder + CSA of Cone
$= 26.4 \text{ m}^2 + 17.6 \text{ m}^2 = 44 \text{ m}^2$
Cost of the canvas:
Cost of canvas = Area of canvas $\times$ Rate per m$^2$
Cost $= 44 \text{ m}^2 \times \textsf{₹} 500/\text{m}^2$
Cost $= \textsf{₹} (44 \times 500)$
Calculate $44 \times 500 = 22000$.
Cost $= \textsf{₹} 22000$
Answer:
The area of the canvas used for making the tent is $44 \text{ m}^2$.
The cost of the canvas of the tent is $\textsf{₹} 22000$.
Question 8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2 .
Answer:
This problem involves removing a conical part from a solid cylinder and finding the total surface area of the remaining solid. The total surface area includes the original base, the curved side, and the newly created inner conical surface.
Given:
A solid cylinder with height $h = 2.4 \text{ cm}$ and diameter $1.4 \text{ cm}$.
A conical cavity of the same height and same diameter is hollowed out from the cylinder.
Value of $\pi = \frac{22}{7}$
To Find:
The total surface area of the remaining solid to the nearest cm$^2$.
Solution:
Diameter of the cylinder and cone = $1.4 \text{ cm}$.
Radius of the cylinder and cone, $r = \frac{\text{Diameter}}{2} = \frac{1.4}{2} \text{ cm} = 0.7 \text{ cm}$.
Height of the cylinder and cone, $h = 2.4 \text{ cm}$.
The total surface area of the remaining solid consists of:
1. The curved surface area (CSA) of the cylinder.
2. The area of the base of the cylinder (since it is a solid cylinder, the base at the bottom remains).
3. The curved surface area (CSA) of the conical cavity that has been hollowed out from the top.
Total Surface Area of remaining solid = CSA of Cylinder + Area of base of Cylinder + CSA of Cone.
Curved Surface Area (CSA) of the Cylinder:
The formula for the CSA of a cylinder is $2\pi r h$.
CSA of Cylinder $= 2 \times \frac{22}{7} \times 0.7 \text{ cm} \times 2.4 \text{ cm}$
$= 2 \times \frac{22}{7} \times \frac{7}{10} \times \frac{24}{10} \text{ cm}^2$
$= 2 \times \frac{22}{\cancel{7}^{1}} \times \frac{\cancel{7}^{1}}{10} \times \frac{24}{10} \text{ cm}^2$
$= \frac{44 \times 24}{100} \text{ cm}^2 = \frac{1056}{100} \text{ cm}^2 = 10.56 \text{ cm}^2$
Area of the base of the Cylinder:
The base of the cylinder is a circle with radius $r = 0.7 \text{ cm}$.
Area of base $= \pi r^2 = \frac{22}{7} \times (0.7 \text{ cm})^2$
$= \frac{22}{7} \times 0.7 \times 0.7 \text{ cm}^2$
$= 22 \times \frac{\cancel{0.7}^{0.1}}{\cancel{7}^{1}} \times 0.7 \text{ cm}^2 = 22 \times 0.1 \times 0.7 \text{ cm}^2 = 2.2 \times 0.7 \text{ cm}^2 = 1.54 \text{ cm}^2$
Curved Surface Area (CSA) of the Cone:
The formula for the CSA of a cone is $\pi r l$, where $l$ is the slant height. We need to calculate the slant height first.
The slant height $l$ is given by the formula $l = \sqrt{r^2 + h^2}$.
Using $r = 0.7 \text{ cm}$ and $h = 2.4 \text{ cm}$:
$l = \sqrt{(0.7)^2 + (2.4)^2} = \sqrt{0.49 + 5.76} = \sqrt{6.25} \text{ cm}$
The square root of $6.25$ is $2.5$.
$l = 2.5 \text{ cm}$
Now, calculate the CSA of the cone:
CSA of Cone $= \pi r l = \frac{22}{7} \times 0.7 \text{ cm} \times 2.5 \text{ cm}$
$= \frac{22}{\cancel{7}^{1}} \times \cancel{0.7}^{0.1} \times 2.5 \text{ cm}^2$
$= 22 \times 0.1 \times 2.5 \text{ cm}^2 = 2.2 \times 2.5 \text{ cm}^2 = 5.5 \text{ cm}^2$
Total Surface Area of the remaining solid:
Total SA = CSA of Cylinder + Area of base of Cylinder + CSA of Cone
$= 10.56 \text{ cm}^2 + 1.54 \text{ cm}^2 + 5.5 \text{ cm}^2$
$= (10.56 + 1.54) \text{ cm}^2 + 5.5 \text{ cm}^2$
$= 12.10 \text{ cm}^2 + 5.5 \text{ cm}^2 = 17.6 \text{ cm}^2$
The problem asks for the area to the nearest cm$^2$. Rounding $17.6$ to the nearest whole number gives $18$.
Rounding $17.6 \text{ cm}^2$ to the nearest cm$^2$ is $18 \text{ cm}^2$.
Answer:
The total surface area of the remaining solid is $17.6 \text{ cm}^2$, which is $18 \text{ cm}^2$ to the nearest cm$^2$.
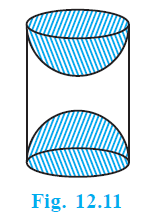
Question 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 12.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
Answer:
This problem involves finding the total surface area of a wooden article formed by scooping out hemispheres from both ends of a solid cylinder. The exposed surfaces are the curved side of the cylinder and the curved surfaces of the two depressions.
Given:
A wooden article made by scooping out a hemisphere from each end of a solid cylinder.
Height of the cylinder, $h = 10 \text{ cm}$
Radius of the base of the cylinder, $r = 3.5 \text{ cm}$
Value of $\pi = \frac{22}{7}$
To Find:
The total surface area of the article.
Solution:
The radius of the hemispherical depressions is the same as the radius of the cylinder's base, $r = 3.5 \text{ cm}$.
The total surface area of the article is the sum of the curved surface area (CSA) of the cylindrical part and the curved surface areas (CSA) of the two hemispherical depressions that were scooped out from the ends. The flat circular ends of the original solid cylinder are replaced by the curved surfaces of the inner hemispheres.
Total Surface Area of article = CSA of Cylinder + CSA of Hemisphere from one end + CSA of Hemisphere from the other end
Total Surface Area = CSA of Cylinder + 2 $\times$ CSA of one Hemisphere
Curved Surface Area (CSA) of the Cylinder:
The formula for the CSA of a cylinder is $2\pi r h$.
Using $r = 3.5 \text{ cm}$ and $h = 10 \text{ cm}$:
CSA of Cylinder $= 2 \times \frac{22}{7} \times 3.5 \text{ cm} \times 10 \text{ cm}$
$= 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{3.5}^{0.5} \times 10 \text{ cm}^2$
$= 44 \times 0.5 \times 10 \text{ cm}^2$
$= 22 \times 10 \text{ cm}^2 = 220 \text{ cm}^2$
Curved Surface Area (CSA) of one Hemisphere:
The formula for the CSA of a hemisphere is $2\pi r^2$.
Using $r = 3.5 \text{ cm}$:
CSA of one Hemisphere $= 2 \times \frac{22}{7} \times (3.5 \text{ cm})^2$
$= 2 \times \frac{22}{7} \times 3.5 \times 3.5 \text{ cm}^2$
$= 2 \times 22 \times \frac{\cancel{3.5}^{0.5}}{\cancel{7}^{1}} \times 3.5 \text{ cm}^2$
$= 44 \times 0.5 \times 3.5 \text{ cm}^2$
$= 22 \times 3.5 \text{ cm}^2 = 77 \text{ cm}^2$
Total Surface Area of the article:
Total SA = CSA of Cylinder + 2 $\times$ CSA of one Hemisphere
$= 220 \text{ cm}^2 + 2 \times 77 \text{ cm}^2$
$= 220 \text{ cm}^2 + 154 \text{ cm}^2 = 374 \text{ cm}^2$
Answer:
The total surface area of the article is $374 \text{ cm}^2$.
Example 5 to 7 (Before Exercise 12.2)
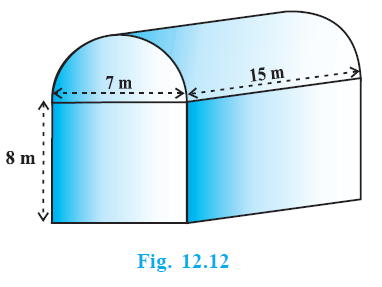
Example 5. Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (see Fig. 12.12). If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m3 , and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then, how much air is in the shed? (Take π = $\frac{22}{7}$ )
Answer:
Given:
The shed is in the shape of a cuboid surmounted by a half cylinder.
Dimensions of the cuboidal base = $7 \text{ m} \times 15 \text{ m}$.
Height of the cuboidal portion = $8 \text{ m}$.
Space occupied by machinery = $300 \text{ m}^3$.
Number of workers = 20.
Space occupied by each worker = $0.08 \text{ m}^3$.
Value of $\pi = \frac{22}{7}$
To Find:
1. The volume of air that the shed can hold (total volume).
2. The amount of air in the shed (total volume minus space occupied by machinery and workers).
Solution:
The shed is composed of a cuboidal part and a half-cylindrical part.
Dimensions of the Cuboidal Part:
Length, $L = 15 \text{ m}$
Breadth, $B = 7 \text{ m}$
Height, $H = 8 \text{ m}$
Volume of Cuboidal part $= L \times B \times H = 15 \text{ m} \times 7 \text{ m} \times 8 \text{ m}$
$= 105 \times 8 \text{ m}^3 = 840 \text{ m}^3$
Dimensions of the Half-Cylindrical Part:
The half-cylinder surmounts the cuboid. The base of the half-cylinder corresponds to the top face of the cuboid.
The diameter of the base of the cylinder is equal to the breadth of the cuboid's top face, which is $7 \text{ m}$.
Diameter of cylinder base = $7 \text{ m}$. Radius of cylinder base, $r = \frac{7}{2} \text{ m} = 3.5 \text{ m}$.
The length of the cylinder is equal to the length of the cuboid's top face, which is $15 \text{ m}$.
Height (length) of the cylinder, $h = 15 \text{ m}$.
Volume of full Cylinder $= \pi r^2 h$
$= \frac{22}{7} \times (3.5 \text{ m})^2 \times 15 \text{ m}$
$= \frac{22}{7} \times 3.5 \times 3.5 \times 15 \text{ m}^3$
$= 22 \times \frac{\cancel{3.5}^{0.5}}{\cancel{7}^{1}} \times 3.5 \times 15 \text{ m}^3$
$= 22 \times 0.5 \times 3.5 \times 15 \text{ m}^3$
$= 11 \times 3.5 \times 15 \text{ m}^3$
$= 38.5 \times 15 \text{ m}^3$
$= 577.5 \text{ m}^3$
Volume of Half-Cylindrical part $= \frac{1}{2} \times \text{Volume of full Cylinder}$
$= \frac{1}{2} \times 577.5 \text{ m}^3 = 288.75 \text{ m}^3$
1. Volume of air that the shed can hold (Total volume):
Total Volume of shed = Volume of Cuboidal part + Volume of Half-Cylindrical part
$= 840 \text{ m}^3 + 288.75 \text{ m}^3$
$= 1128.75 \text{ m}^3$
2. Amount of air in the shed:
Space occupied by machinery $= 300 \text{ m}^3$.
Space occupied by 20 workers $= 20 \times 0.08 \text{ m}^3 = 1.6 \text{ m}^3$.
Total space occupied by machinery and workers $= 300 \text{ m}^3 + 1.6 \text{ m}^3 = 301.6 \text{ m}^3$.
Amount of air in the shed = Total Volume of shed - Total space occupied by machinery and workers
$= 1128.75 \text{ m}^3 - 301.6 \text{ m}^3$
$= 827.15 \text{ m}^3$
Answer:
1. The volume of air that the shed can hold is $1128.75 \text{ m}^3$.
2. The amount of air in the shed is $827.15 \text{ m}^3$.
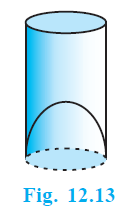
Example 6. A juice seller was serving his customers using glasses as shown in Fig. 12.13. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14.)
Answer:
Given:
The glass is in the shape of a cylinder with a hemispherical raised portion at the bottom.
Inner diameter of the cylindrical glass = $5 \text{ cm}$.
Height of the glass, $h = 10 \text{ cm}$.
Value of $\pi = 3.14$.
To Find:
1. The apparent capacity of the glass.
2. The actual capacity of the glass.
Solution:
The inner diameter of the cylindrical glass is $5 \text{ cm}$.
Inner radius of the cylindrical glass, $r = \frac{5}{2} \text{ cm} = 2.5 \text{ cm}$.
The height of the glass is $h = 10 \text{ cm}$.
The hemispherical raised portion at the bottom has the same radius as the cylinder, $r = 2.5 \text{ cm}$.
1. Apparent capacity of the glass:
The apparent capacity of the glass is the volume of the cylinder with the given height and inner diameter.
Volume of cylinder $= \pi r^2 h$
$= 3.14 \times (2.5 \text{ cm})^2 \times 10 \text{ cm}$
$= 3.14 \times 6.25 \text{ cm}^2 \times 10 \text{ cm}$
$= 3.14 \times 62.5 \text{ cm}^3$
$= 196.25 \text{ cm}^3$
2. Actual capacity of the glass:
The actual capacity of the glass is the volume of the cylinder minus the volume of the hemispherical raised portion at the bottom.
Volume of hemisphere $= \frac{2}{3}\pi r^3$
$= \frac{2}{3} \times 3.14 \times (2.5 \text{ cm})^3$
$= \frac{2}{3} \times 3.14 \times 15.625 \text{ cm}^3$
$= \frac{2 \times 3.14 \times 15.625}{3} \text{ cm}^3$
$= \frac{6.28 \times 15.625}{3} \text{ cm}^3$
$= \frac{98.125}{3} \text{ cm}^3$
$\approx 32.7083 \text{ cm}^3$
Actual capacity = Volume of cylinder - Volume of hemisphere
$= 196.25 \text{ cm}^3 - \frac{98.125}{3} \text{ cm}^3$
$= 196.25 - 32.7083 \text{ cm}^3$
$= 163.5417 \text{ cm}^3$
Rounding to two decimal places:
Actual capacity $\approx 163.54 \text{ cm}^3$
Answer:
The apparent capacity of the glass is $196.25 \text{ cm}^3$.
The actual capacity of the glass is approximately $163.54 \text{ cm}^3$.
Example 7. A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)
Answer:
This problem involves a solid toy made of a hemisphere and a cone. We need to find its volume and compare it with the volume of a cylinder that perfectly encloses it.
Given:
A solid toy in the form of a hemisphere surmounted by a right circular cone.
Height of the cone, $h_c = 2 \text{ cm}$.
Diameter of the base = $4 \text{ cm}$.
Value of $\pi = 3.14$.
To Find:
1. The volume of the toy.
2. The difference in volumes between a circumscribing cylinder and the toy.
Solution:
The toy is composed of a hemisphere and a cone sharing the same base.
The diameter of the base of the cone is $4 \text{ cm}$.
The radius of the base of the cone, $r = \frac{\text{Diameter}}{2} = \frac{4}{2} \text{ cm} = 2 \text{ cm}$.
Since the cone is placed on the hemisphere and they have the same base, the radius of the hemisphere is also $r = 2 \text{ cm}$.
The height of the hemispherical part is equal to its radius, which is $2 \text{ cm}$.
The height of the cone is given as $h_c = 2 \text{ cm}$.
1. Volume of the toy:
The volume of the toy is the sum of the volume of the hemisphere and the volume of the cone.
Formula for Volume of hemisphere $= \frac{2}{3}\pi r^3$
Volume of hemisphere $= \frac{2}{3} \times 3.14 \times (2 \text{ cm})^3$
$= \frac{2}{3} \times 3.14 \times 8 \text{ cm}^3$
$= \frac{16 \times 3.14}{3} \text{ cm}^3 = \frac{50.24}{3} \text{ cm}^3$
Formula for Volume of cone $= \frac{1}{3}\pi r^2 h_c$
Volume of cone $= \frac{1}{3} \times 3.14 \times (2 \text{ cm})^2 \times 2 \text{ cm}$
$= \frac{1}{3} \times 3.14 \times 4 \times 2 \text{ cm}^3$
$= \frac{8 \times 3.14}{3} \text{ cm}^3 = \frac{25.12}{3} \text{ cm}^3$
Volume of toy = Volume of hemisphere + Volume of cone
$= \frac{50.24}{3} \text{ cm}^3 + \frac{25.12}{3} \text{ cm}^3$
$= \frac{50.24 + 25.12}{3} \text{ cm}^3$
$= \frac{75.36}{3} \text{ cm}^3$
Performing the division:
$\frac{75.36}{3} = 25.12$
Volume of toy $= 25.12 \text{ cm}^3$
2. Difference of volumes between a circumscribing cylinder and the toy:
A right circular cylinder that circumscribes the toy would have the same base radius as the toy and a height equal to the maximum height of the toy (from the base of the hemisphere to the tip of the cone).
Radius of the circumscribing cylinder, $r = 2 \text{ cm}$ (same as the toy's base radius).
The total height of the toy is the sum of the height of the hemisphere and the height of the cone.
Total height of toy = Height of hemisphere + Height of cone
Total height $= 2 \text{ cm} + 2 \text{ cm} = 4 \text{ cm}$.
Height of the circumscribing cylinder, $h_y = 4 \text{ cm}$.
Formula for Volume of circumscribing cylinder $= \pi r^2 h_y$
Volume of circumscribing cylinder $= 3.14 \times (2 \text{ cm})^2 \times 4 \text{ cm}$
$= 3.14 \times 4 \times 4 \text{ cm}^3$
$= 3.14 \times 16 \text{ cm}^3$
Performing the multiplication: $3.14 \times 16 = 50.24$
Volume of circumscribing cylinder $= 50.24 \text{ cm}^3$
The difference in volumes is the volume of the cylinder minus the volume of the toy.
Difference in volumes = Volume of cylinder - Volume of toy
$= 50.24 \text{ cm}^3 - 25.12 \text{ cm}^3$
Performing the subtraction: $50.24 - 25.12 = 25.12$
Difference in volumes $= 25.12 \text{ cm}^3$
Answer:
1. The volume of the toy is $25.12 \text{ cm}^3$.
2. The difference of the volumes of the cylinder and the toy is $25.12 \text{ cm}^3$.
Exercise 12.2
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Answer:
Given:
A solid in the shape of a cone standing on a hemisphere.
Radius of cone = Radius of hemisphere, $r = 1 \text{ cm}$.
Height of the cone = Radius of the cone, $h = r = 1 \text{ cm}$.
The answer is required in terms of $\pi$.
To Find:
The volume of the solid.
Solution:
The volume of the solid is the sum of the volume of the cone and the volume of the hemisphere.
Radius of hemisphere, $r = 1 \text{ cm}$.
Volume of hemisphere $= \frac{2}{3}\pi r^3$
$= \frac{2}{3}\pi (1 \text{ cm})^3$
$= \frac{2}{3}\pi \times 1 \text{ cm}^3$
$= \frac{2}{3}\pi \text{ cm}^3$
Radius of cone, $r = 1 \text{ cm}$.
Height of cone, $h = 1 \text{ cm}$.
Volume of cone $= \frac{1}{3}\pi r^2 h$
$= \frac{1}{3}\pi (1 \text{ cm})^2 (1 \text{ cm})$
$= \frac{1}{3}\pi \times 1 \times 1 \text{ cm}^3$
$= \frac{1}{3}\pi \text{ cm}^3$
Volume of solid = Volume of cone + Volume of hemisphere
$= \frac{1}{3}\pi \text{ cm}^3 + \frac{2}{3}\pi \text{ cm}^3$
$= (\frac{1}{3} + \frac{2}{3})\pi \text{ cm}^3$
$= \frac{3}{3}\pi \text{ cm}^3$
$= 1\pi \text{ cm}^3 = \pi \text{ cm}^3$
Answer:
The volume of the solid is $\pi \text{ cm}^3$.
Question 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Answer:
Given:
The model is shaped like a cylinder with two cones attached at its ends.
Diameter of the model = $3 \text{ cm}$.
Length of the model = $12 \text{ cm}$.
Height of each cone = $2 \text{ cm}$.
Value of $\pi = \frac{22}{7}$
To Find:
The volume of air contained in the model.
Solution:
The model consists of a cylindrical part and two conical parts at the ends.
Diameter of the model = $3 \text{ cm}$.
Radius of the cylindrical and conical parts, $r = \frac{3}{2} \text{ cm} = 1.5 \text{ cm}$.
Total length of the model = $12 \text{ cm}$.
Height of each cone, $h_c = 2 \text{ cm}$.
The length of the cylindrical part is the total length of the model minus the heights of the two cones.
Height of the cylindrical part, $h_y = \text{Total length} - (\text{Height of cone 1} + \text{Height of cone 2})$
$h_y = 12 \text{ cm} - (2 \text{ cm} + 2 \text{ cm})$
$h_y = 12 \text{ cm} - 4 \text{ cm} = 8 \text{ cm}$.
The volume of air contained in the model is the sum of the volume of the cylinder and the volumes of the two cones.
Volume of model = Volume of Cylinder + Volume of Cone 1 + Volume of Cone 2
Volume of model = Volume of Cylinder + 2 $\times$ Volume of Cone
Volume of the Cylinder:
The formula for the volume of a cylinder is $\pi r^2 h_y$.
$r = 1.5 \text{ cm}$ and $h_y = 8 \text{ cm}$.
Volume of Cylinder $= \frac{22}{7} \times (1.5 \text{ cm})^2 \times 8 \text{ cm}$
$= \frac{22}{7} \times 2.25 \times 8 \text{ cm}^3$
$= \frac{22}{7} \times 18 \text{ cm}^3 = \frac{396}{7} \text{ cm}^3$
Volume of one Cone:
The formula for the volume of a cone is $\frac{1}{3}\pi r^2 h_c$.
$r = 1.5 \text{ cm}$ and $h_c = 2 \text{ cm}$.
Volume of one Cone $= \frac{1}{3} \times \frac{22}{7} \times (1.5 \text{ cm})^2 \times 2 \text{ cm}$
$= \frac{1}{3} \times \frac{22}{7} \times 2.25 \times 2 \text{ cm}^3$
$= \frac{1}{3} \times \frac{22}{7} \times 4.5 \text{ cm}^3$
$= \frac{22}{7} \times \frac{\cancel{4.5}^{1.5}}{\cancel{3}^{1}} \text{ cm}^3 = \frac{22}{7} \times 1.5 \text{ cm}^3 = \frac{33}{7} \text{ cm}^3$
Volume of the model:
Volume of model = Volume of Cylinder + 2 $\times$ Volume of one Cone
$= \frac{396}{7} \text{ cm}^3 + 2 \times \frac{33}{7} \text{ cm}^3$
$= \frac{396}{7} \text{ cm}^3 + \frac{66}{7} \text{ cm}^3$
$= \frac{396 + 66}{7} \text{ cm}^3$
$= \frac{462}{7} \text{ cm}^3$
$= 66 \text{ cm}^3$
Answer:
The volume of air contained in the model is $66 \text{ cm}^3$.
Question 3. A gulab jamun,contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns,each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig. 12.15).
Answer:
Given:
Percentage of sugar syrup in a gulab jamun = 30% of its volume.
Number of gulab jamuns = 45.
Shape of each gulab jamun: cylinder with two hemispherical ends.
Length of each gulab jamun = $5 \text{ cm}$.
Diameter of each gulab jamun = $2.8 \text{ cm}$.
Value of $\pi = \frac{22}{7}$
To Find:
Approximately how much syrup would be found in 45 gulab jamuns.
Solution:
First, we need to find the volume of a single gulab jamun.
The shape is a cylinder with two hemispherical ends.
Diameter of the gulab jamun = $2.8 \text{ cm}$.
Radius of the cylindrical and hemispherical parts, $r = \frac{2.8}{2} \text{ cm} = 1.4 \text{ cm}$.
The height of each hemispherical part is equal to its radius, which is $1.4 \text{ cm}$.
Total length of the gulab jamun = $5 \text{ cm}$.
The length of the cylindrical part is the total length of the gulab jamun minus the heights of the two hemispherical ends.
Height (length) of the cylindrical part, $h = \text{Total length} - (\text{Height of one hemisphere} + \text{Height of other hemisphere})$
$h = 5 \text{ cm} - (1.4 \text{ cm} + 1.4 \text{ cm})$
$h = 5 \text{ cm} - 2.8 \text{ cm} = 2.2 \text{ cm}$.
The volume of one gulab jamun is the sum of the volume of the cylindrical part and the volumes of the two hemispherical ends.
Volume of one gulab jamun = Volume of Cylinder + Volume of two Hemispheres
Volume of one gulab jamun = Volume of Cylinder + 2 $\times$ Volume of one Hemisphere
Volume of the Cylinder:
The formula for the volume of a cylinder is $\pi r^2 h$.
$r = 1.4 \text{ cm}$ and $h = 2.2 \text{ cm}$.
Volume of Cylinder $= \frac{22}{7} \times (1.4 \text{ cm})^2 \times 2.2 \text{ cm}$
$= \frac{22}{7} \times 1.96 \times 2.2 \text{ cm}^3$
$= 22 \times \frac{\cancel{1.96}^{0.28}}{\cancel{7}^{1}} \times 2.2 \text{ cm}^3$
$= 22 \times 0.28 \times 2.2 \text{ cm}^3$
$= 6.16 \times 2.2 \text{ cm}^3$
$= 13.552 \text{ cm}^3$
Volume of one Hemisphere:
The formula for the volume of a hemisphere is $\frac{2}{3}\pi r^3$.
$r = 1.4 \text{ cm}$.
Volume of one Hemisphere $= \frac{2}{3} \times \frac{22}{7} \times (1.4 \text{ cm})^3$
$= \frac{2}{3} \times \frac{22}{7} \times 1.4 \times 1.4 \times 1.4 \text{ cm}^3$
$= \frac{44}{21} \times 2.744 \text{ cm}^3$
Using fraction form: $r=1.4 = \frac{14}{10} = \frac{7}{5}$.
Volume of one Hemisphere $= \frac{2}{3} \times \frac{22}{7} \times (\frac{7}{5})^3 \text{ cm}^3 = \frac{2}{3} \times \frac{22}{7} \times \frac{343}{125} \text{ cm}^3$
$= \frac{44}{3} \times \frac{\cancel{343}^{49}}{\cancel{7}^{1} \times 125} \text{ cm}^3 = \frac{44 \times 49}{3 \times 125} \text{ cm}^3 = \frac{2156}{375} \text{ cm}^3$
Volume of two Hemispheres $= 2 \times \frac{2156}{375} \text{ cm}^3 = \frac{4312}{375} \text{ cm}^3$
Using fraction form for cylindrical volume: $r = \frac{7}{5}$, $h = 2.2 = \frac{22}{10} = \frac{11}{5}$.
Volume of Cylinder $= \pi r^2 h = \frac{22}{7} \times (\frac{7}{5})^2 \times \frac{11}{5} \text{ cm}^3 = \frac{22}{7} \times \frac{49}{25} \times \frac{11}{5} \text{ cm}^3$
$= \frac{22}{\cancel{7}^{1}} \times \frac{\cancel{49}^{7}}{25} \times \frac{11}{5} \text{ cm}^3 = \frac{22 \times 7 \times 11}{25 \times 5} \text{ cm}^3 = \frac{154 \times 11}{125} \text{ cm}^3 = \frac{1694}{125} \text{ cm}^3$
Volume of one gulab jamun = Volume of Cylinder + Volume of two Hemispheres
$= \frac{1694}{125} \text{ cm}^3 + \frac{4312}{375} \text{ cm}^3$
Find a common denominator (375):
Volume of one gulab jamun $= \frac{1694 \times 3}{125 \times 3} \text{ cm}^3 + \frac{4312}{375} \text{ cm}^3 = \frac{5082}{375} \text{ cm}^3 + \frac{4312}{375} \text{ cm}^3$
$= \frac{5082 + 4312}{375} \text{ cm}^3 = \frac{9394}{375} \text{ cm}^3$
Total volume of 45 gulab jamuns:
Total Volume $= 45 \times \text{Volume of one gulab jamun}$
$= 45 \times \frac{9394}{375} \text{ cm}^3$
$= \frac{\cancel{45}^{9} \times 9394}{\cancel{375}^{75}} \text{ cm}^3$
$= \frac{\cancel{9}^{3} \times 9394}{\cancel{75}^{25}} \text{ cm}^3$
$= \frac{3 \times 9394}{25} \text{ cm}^3 = \frac{28182}{25} \text{ cm}^3 = 1127.28 \text{ cm}^3$
Amount of sugar syrup:
Amount of syrup = 30% of Total Volume
$= 30\% \times 1127.28 \text{ cm}^3$
$= \frac{30}{100} \times 1127.28 \text{ cm}^3 = 0.3 \times 1127.28 \text{ cm}^3$
$= 338.184 \text{ cm}^3$
The question asks for the approximate amount of syrup.
Answer:
Approximately $338 \text{ cm}^3$ (or $338.18 \text{ cm}^3$) of sugar syrup would be found in 45 gulab jamuns.
Question 4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 12.16).
Answer:
Given:
The pen stand is a cuboid with four conical depressions.
Dimensions of the cuboid: Length, $L = 15 \text{ cm}$, Breadth, $B = 10 \text{ cm}$, Height, $H = 3.5 \text{ cm}$.
Number of conical depressions = 4.
Radius of each conical depression, $r = 0.5 \text{ cm}$.
Depth (height) of each conical depression, $h = 1.4 \text{ cm}$.
Value of $\pi = \frac{22}{7}$
To Find:
The volume of wood in the entire stand.
Solution:
The volume of the wood in the pen stand is the volume of the cuboid minus the total volume of the four conical depressions.
Volume of wood = Volume of Cuboid - Total Volume of 4 Conical Depressions.
Volume of the Cuboid:
The formula for the volume of a cuboid is $L \times B \times H$.
Volume of Cuboid $= 15 \text{ cm} \times 10 \text{ cm} \times 3.5 \text{ cm}$
$= 150 \times 3.5 \text{ cm}^3$
$= 525 \text{ cm}^3$
Volume of one Conical Depression:
The formula for the volume of a cone is $\frac{1}{3}\pi r^2 h$.
$r = 0.5 \text{ cm}$ and $h = 1.4 \text{ cm}$.
Volume of one cone $= \frac{1}{3} \times \frac{22}{7} \times (0.5 \text{ cm})^2 \times 1.4 \text{ cm}$
$= \frac{1}{3} \times \frac{22}{7} \times 0.25 \times 1.4 \text{ cm}^3$
$= \frac{1}{3} \times \frac{22}{\cancel{7}^{1}} \times 0.25 \times \cancel{1.4}^{0.2} \text{ cm}^3$
$= \frac{1}{3} \times 22 \times 0.25 \times 0.2 \text{ cm}^3$
$= \frac{1}{3} \times 22 \times 0.05 \text{ cm}^3$
$= \frac{1.1}{3} \text{ cm}^3$
Total Volume of 4 Conical Depressions:
Total Volume of cones $= 4 \times (\text{Volume of one cone})$
$= 4 \times \frac{1.1}{3} \text{ cm}^3 = \frac{4.4}{3} \text{ cm}^3$
Volume of wood in the entire stand:
Volume of wood = Volume of Cuboid - Total Volume of 4 Conical Depressions
$= 525 \text{ cm}^3 - \frac{4.4}{3} \text{ cm}^3$
$= 525 - \frac{4.4}{3} \text{ cm}^3$
To subtract, find a common denominator:
$= \frac{525 \times 3}{3} \text{ cm}^3 - \frac{4.4}{3} \text{ cm}^3$
$= \frac{1575 - 4.4}{3} \text{ cm}^3$
$= \frac{1570.6}{3} \text{ cm}^3$
Performing the division:
$1570.6 \div 3 \approx 523.533...$
Volume of wood $\approx 523.53 \text{ cm}^3$ (rounding to two decimal places)
Answer:
The volume of wood in the entire stand is $\frac{1570.6}{3} \text{ cm}^3$ or approximately $523.53 \text{ cm}^3$.
Question 5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer:
Given:
The vessel is in the form of an inverted cone.
Height of the cone, $h = 8 \text{ cm}$.
Radius of the top (open) of the cone, $R = 5 \text{ cm}$.
The cone is filled with water up to the brim.
Lead shots (spheres) are dropped into the vessel.
Radius of each lead shot, $r = 0.5 \text{ cm}$.
One-fourth of the water flows out when lead shots are dropped.
Value of $\pi = \frac{22}{7}$ (standard assumption unless otherwise stated)
To Find:
The number of lead shots dropped in the vessel.
Solution:
When lead shots are dropped into the vessel, the volume of water that flows out is equal to the total volume of the lead shots dropped, as long as they are fully submerged.
First, calculate the volume of the cone (which is the initial volume of water).
Volume of cone $= \frac{1}{3}\pi R^2 h$
$= \frac{1}{3} \times \pi \times (5 \text{ cm})^2 \times 8 \text{ cm}$
$= \frac{1}{3} \times \pi \times 25 \times 8 \text{ cm}^3$
$= \frac{200\pi}{3} \text{ cm}^3$
The volume of water that flows out is one-fourth of the volume of the cone.
Volume of water flowed out $= \frac{1}{4} \times \text{Volume of cone}$
$= \frac{1}{4} \times \frac{200\pi}{3} \text{ cm}^3$
$= \frac{\cancel{200}^{50}\pi}{\cancel{4}^{1} \times 3} \text{ cm}^3 = \frac{50\pi}{3} \text{ cm}^3$
Next, calculate the volume of one lead shot (sphere).
The formula for the volume of a sphere is $\frac{4}{3}\pi r^3$.
$r = 0.5 \text{ cm}$.
Volume of one lead shot $= \frac{4}{3}\pi (0.5 \text{ cm})^3$
$= \frac{4}{3}\pi \times (0.5)^3 \text{ cm}^3$
$= \frac{4}{3}\pi \times 0.125 \text{ cm}^3$
$= \frac{0.5\pi}{3} \text{ cm}^3$
Let $N$ be the number of lead shots dropped into the vessel.
The total volume of $N$ lead shots is $N \times (\text{Volume of one lead shot})$.
Total volume of lead shots $= N \times \frac{0.5\pi}{3} \text{ cm}^3 = \frac{0.5 N \pi}{3} \text{ cm}^3$
The volume of water flowed out is equal to the total volume of the lead shots dropped.
$\text{Volume of water flowed out} = \text{Total volume of lead shots}$
... (i)
$\frac{50\pi}{3} = \frac{0.5 N \pi}{3}$
Cancel $\frac{\pi}{3}$ from both sides:
$50 = 0.5 N$
To find $N$, divide 50 by 0.5:
$N = \frac{50}{0.5}$
$N = \frac{50}{\frac{1}{2}}$
$N = 50 \times 2 = 100$
So, 100 lead shots were dropped in the vessel.
Answer:
The number of lead shots dropped in the vessel is 100.
Question 6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8g mass. (Use π = 3.14)
Answer:
Given:
The solid iron pole consists of two cylinders one above the other.
Lower cylinder: Height, $h_1 = 220 \text{ cm}$. Base diameter = $24 \text{ cm}$.
Upper cylinder: Height, $h_2 = 60 \text{ cm}$. Radius, $r_2 = 8 \text{ cm}$.
Mass of $1 \text{ cm}^3$ of iron = $8 \text{ g}$.
Value of $\pi = 3.14$.
To Find:
The mass of the pole.
Solution:
First, we need to find the total volume of the iron pole, which is the sum of the volumes of the two cylinders.
Lower Cylinder:
Base diameter = $24 \text{ cm}$. Radius, $r_1 = \frac{24}{2} \text{ cm} = 12 \text{ cm}$.
Height, $h_1 = 220 \text{ cm}$.
Volume of lower cylinder $= \pi r_1^2 h_1$
$= 3.14 \times (12 \text{ cm})^2 \times 220 \text{ cm}$
$= 3.14 \times 144 \times 220 \text{ cm}^3$
$= 3.14 \times 31680 \text{ cm}^3$
$= 99532.8 \text{ cm}^3$
Upper Cylinder:
Radius, $r_2 = 8 \text{ cm}$.
Height, $h_2 = 60 \text{ cm}$.
Volume of upper cylinder $= \pi r_2^2 h_2$
$= 3.14 \times (8 \text{ cm})^2 \times 60 \text{ cm}$
$= 3.14 \times 64 \times 60 \text{ cm}^3$
$= 3.14 \times 3840 \text{ cm}^3$
$= 12057.6 \text{ cm}^3$
Total Volume of the pole:
Total Volume = Volume of lower cylinder + Volume of upper cylinder
$= 99532.8 \text{ cm}^3 + 12057.6 \text{ cm}^3$
$= 111590.4 \text{ cm}^3$
Mass of the pole:
Mass = Total Volume $\times$ Mass per unit volume
Mass $= 111590.4 \text{ cm}^3 \times 8 \text{ g/cm}^3$
$= (111590.4 \times 8) \text{ g}$
Mass $= 892723.2 \text{ g}$
To convert grams to kilograms, divide by 1000.
Mass in kg $= \frac{892723.2}{1000} \text{ kg}$
Mass in kg $= 892.7232 \text{ kg}$
Answer:
The mass of the pole is $892723.2 \text{ g}$ or $892.7232 \text{ kg}$.
Question 7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Answer:
Given:
A solid consisting of a right circular cone standing on a hemisphere.
Cone: Height, $h_c = 120 \text{ cm}$, Radius, $r = 60 \text{ cm}$.
Hemisphere: Radius, $r = 60 \text{ cm}$.
The solid is placed upright in a right circular cylinder full of water.
Cylinder: Radius, $R = 60 \text{ cm}$, Height, $H = 180 \text{ cm}$.
The solid touches the bottom of the cylinder.
Value of $\pi = \frac{22}{7}$
To Find:
The volume of water left in the cylinder.
Solution:
The volume of water left in the cylinder is the volume of the cylinder minus the volume of the solid placed in it.
Radius of cone base = Radius of hemisphere = Radius of cylinder base = $60 \text{ cm}$.
Height of cone = $120 \text{ cm}$.
Height of hemisphere = its radius = $60 \text{ cm}$.
Total height of the solid = Height of cone + Height of hemisphere
Total height of solid $= 120 \text{ cm} + 60 \text{ cm} = 180 \text{ cm}$.
This height is equal to the height of the cylinder, which means the top of the cone touches the top surface of the water when the solid is placed in the full cylinder.
Volume of the Solid:
The volume of the solid is the sum of the volume of the cone and the volume of the hemisphere.
Volume of cone $= \frac{1}{3}\pi r^2 h_c$
$= \frac{1}{3} \times \pi \times (60 \text{ cm})^2 \times 120 \text{ cm}$
$= \frac{1}{3} \times \pi \times 3600 \times 120 \text{ cm}^3$
$= \pi \times 3600 \times \frac{\cancel{120}^{40}}{\cancel{3}^{1}} \text{ cm}^3$
$= \pi \times 3600 \times 40 \text{ cm}^3 = 144000\pi \text{ cm}^3$
Volume of hemisphere $= \frac{2}{3}\pi r^3$
$= \frac{2}{3} \times \pi \times (60 \text{ cm})^3$
$= \frac{2}{3} \times \pi \times 216000 \text{ cm}^3$
$= 2\pi \times \frac{\cancel{216000}^{72000}}{\cancel{3}^{1}} \text{ cm}^3 = 2\pi \times 72000 \text{ cm}^3 = 144000\pi \text{ cm}^3$
Volume of solid = Volume of cone + Volume of hemisphere
$= 144000\pi \text{ cm}^3 + 144000\pi \text{ cm}^3 = 288000\pi \text{ cm}^3$
Volume of the Cylinder:
The formula for the volume of a cylinder is $\pi R^2 H$.
$R = 60 \text{ cm}$ and $H = 180 \text{ cm}$.
Volume of cylinder $= \pi \times (60 \text{ cm})^2 \times 180 \text{ cm}$
$= \pi \times 3600 \times 180 \text{ cm}^3$
$= 648000\pi \text{ cm}^3$
Volume of water left in the cylinder:
Volume of water left = Volume of cylinder - Volume of solid
$= 648000\pi \text{ cm}^3 - 288000\pi \text{ cm}^3$
$= (648000 - 288000)\pi \text{ cm}^3$
$= 360000\pi \text{ cm}^3$
Now substitute the value of $\pi = \frac{22}{7}$ (as per the general instruction for the exercise).
Volume of water left $= 360000 \times \frac{22}{7} \text{ cm}^3$
$= \frac{7920000}{7} \text{ cm}^3$
Answer:
The volume of water left in the cylinder is $360000\pi \text{ cm}^3$ or $\frac{7920000}{7} \text{ cm}^3$.
Question 8. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3 . Check whether she is correct, taking the above as the inside measurements, and π= 3.14.
Answer:
Given:
A spherical glass vessel with a cylindrical neck.
Cylindrical neck: Height, $h = 8 \text{ cm}$, Diameter = $2 \text{ cm}$.
Spherical part: Diameter = $8.5 \text{ cm}$.
Child's measured volume = $345 \text{ cm}^3$.
Value of $\pi = 3.14$.
To Check:
Whether the child's measured volume is correct by calculating the actual volume of the vessel using the given inside measurements.
Solution:
The volume of the glass vessel is the sum of the volume of the cylindrical neck and the volume of the spherical part.
Volume of vessel = Volume of Cylinder + Volume of Sphere.
Cylindrical neck:
Diameter = $2 \text{ cm}$. Radius, $r = \frac{2}{2} \text{ cm} = 1 \text{ cm}$.
Height, $h = 8 \text{ cm}$.
Volume of cylinder $= \pi r^2 h$
$= 3.14 \times (1 \text{ cm})^2 \times 8 \text{ cm}$
$= 3.14 \times 1 \times 8 \text{ cm}^3$
$= 25.12 \text{ cm}^3$
Spherical part:
Diameter = $8.5 \text{ cm}$. Radius, $R = \frac{8.5}{2} \text{ cm} = 4.25 \text{ cm}$.
Volume of sphere $= \frac{4}{3}\pi R^3$
$= \frac{4}{3} \times 3.14 \times (4.25 \text{ cm})^3$
$= \frac{4}{3} \times 3.14 \times (4.25 \times 4.25 \times 4.25) \text{ cm}^3$
$= \frac{4}{3} \times 3.14 \times 76.765625 \text{ cm}^3$
$= \frac{12.56 \times 76.765625}{3} \text{ cm}^3$
$= \frac{964.3375}{3} \text{ cm}^3$
$\approx 321.44583 \text{ cm}^3$
Total Volume of the vessel:
Total Volume = Volume of Cylinder + Volume of Sphere
$= 25.12 \text{ cm}^3 + \frac{964.3375}{3} \text{ cm}^3$
$= 25.12 + 321.44583 \text{ cm}^3$ (using approximate value for sphere volume)
$\approx 346.56583 \text{ cm}^3$
Rounding to two decimal places: $\approx 346.57 \text{ cm}^3$.
Comparing with the child's measured volume:
Child's measured volume = $345 \text{ cm}^3$.
Calculated volume $\approx 346.57 \text{ cm}^3$.
The child's measured volume ($345 \text{ cm}^3$) is not exactly equal to the calculated volume ($\approx 346.57 \text{ cm}^3$). There is a difference of approximately $1.57 \text{ cm}^3$.
Conclusion:
The calculated volume of the vessel is approximately $346.57 \text{ cm}^3$. The child found the volume to be $345 \text{ cm}^3$. These values are not exactly equal.
Answer:
No, the child is not correct. The calculated volume of the vessel is approximately $346.57 \text{ cm}^3$, which is different from $345 \text{ cm}^3$.

